Mesurer des Selfs inconnues
Mesurer des Selfs inconnues
![inductances diverses... inductances [283x229px] ombre](/images/stories/Articles/Mesure/Manipulations/inductances_[283x229px]_ombre.png)
Un moyen simple et rapide pour évaluer assez précisément l'inductance d'un inducteur de puissance inconnue.
(à condition d'avoir un générateur de fonctions et un oscilloscope)
D'après une idée originale de Ronald DEKKER.
En cherchant comment mesurer facilement et pour pas trop cher des selfs (inductances en utilisant les bons termes...), mon moteur de recherche préféré que je ne citerai pas ici m'a mené après très peu de temps sur le site Internet de Jean-Louis Naudin 1 , et ensuite sur celui de Ronald DEKKER 2 .
J'avoue avoir été très surpris par la simplicité de la méthode employée, et après quelques essais fructueux, j'ai été rapidement convaincu !
→ Cette technique ne permet de mesurer cependant que des inductances comprises entre quelques dizaines de µH à quelques centaines de µH. En dessous de ces valeurs, il faudrait utiliser une technique de mesure utilisant un générateur de courant du fait de la très faible réactance qui fait que l'inductance représente quasiment un court-circuit au vu de la sortie du GBF, et d'autre part pour dépasser ces valeurs il faudrait un générateur capable de "monter" quasiment jusqu'à 100MHz...
Nous avons tous des inductances de toutes provenances (principalement d'alimentations à découpage pour ma part...) qui une fois démontées de leur circuit imprimé d'origine vont remplir nos tiroirs. La plupart du temps, leur valeur n'est pas inscrite, sauf pour quelques exceptions (Figure 1)...
Il peut devenir intéressant de connaître la valeur d'une inductance, par exemple lors de la conception et/ou modification d'une alimentation, en vue par exemple d'en améliorer la CEM, voire la conception d'un convertisseur élévateur/abaisseur de tension.
«... La compatibilité électromagnétique (CEM) est l'aptitude d'un appareil ou d'un système électrique, ou électronique, à fonctionner dans son environnement électromagnétique de façon satisfaisante, sans produire lui-même des perturbations électromagnétiques intolérables pour tout ce qui se trouve dans cet environnement. ...»3
Voici donc le détail de leur méthode :
En ce qui concerne la partie pûrement théorique, merci de vous rapprocher de celle décrite par Ronald DEKKER.
Ici, point de mathématiques ou de calculs compliqués, que du pratique ! Toutefois, pour les plus curieux, je vais tout de même tenter d'expliquer le principe utilisé en fin d'article.
Tout ce dont vous avez besoin se résume ainsi :
- un générateur de fonctions en mode sinusoïdal
- un oscilloscope (pas nécessairement Digital...)
- éventuellement un fréquencemètre (relié à la sortie TTL du générateur avec un câble BNC/BNC type RG58C/U (50 Ω) ...)
- un (ou deux) câble BNC/BNC type RG58C/U (50 Ω) le plus court possible, le mien mesure 45cm
(par exemple : AMPHENOL - 779829-58-0.6) - un adaptateur BNC type T
(par exemple : TE CONNECTIVITY / GREENPAR - 5-1634532-1) - un adaptateur BNC mâle - 2 Banane Femelle
(par exemple : MULTICOMP - SPC20527) - une simple calculatrice
La méthode étape par étape :

- Connectez la sortie de 50 Ω du générateur de fonctions à l'oscilloscope à l'aide d'un câble approprié (voir ci-dessus), et sélectionnez un signal sinusoïdal.
- Ajuster la fréquence du générateur à environ 20 KHz.
- Ajuster la tension de sortie du générateur à 1 V crête-crête.
- Ajustez la base de temps de l'oscilloscope à 10 µs / division.
- Ajustez le niveau d'entrée de l'ampli vertical CH1 à 200 mV /div.
(si votre écran est gradué comme sur mon HAMEG HM-407, l'amplitude maxi du signal se situera alors entre les 2 niveaux 0 % et 100 %, soit 5 divisions) - Connectez l'inductance inconnue en parallèle sur l'entrée CH1 de l'oscilloscope grâce à l'adaptateur BNC-Banane (Figure 2).
ATTENTION : les connexions de la self à tester doivent être les plus courtes possibles, c'est pourquoi ma self est montée directement sur l'adaptateur BNC. Des connexions trop longues et trop fines risquent de modifier l'impédance totale du circuit RL, et probablement aussi ramener des capacités parasites !
Le signal va diminuer (peut-être même ne verrez-vous quasiment plus le signal sinusoïdal...) puisque celle-ci est directement connectée en parallèle sur CH1. - Ajustez le niveau d'entrée de l'ampli vertical CH1 à 100 mV /div. (Figure 4)
- Maintenant ajustez seulement la fréquence du générateur de telle sorte que l'amplitude sur l'oscilloscope soit exactement la moitié de la valeur d'origine (500 mV c/c, cela correspond à une atténuation de 6dB).

Figure 3 - Enfin, lire la fréquence affichée sur le générateur ou le fréquencemètre (Figure 5), et calculer la valeur de l'inductance selon la formule de Ronald DEKKER : [ L = 4,57 / ƒ ]. Avec L en Henry et ƒ en Hz.
Vous pouvez également préférer L = 4570 / ƒ avec L en µH et ƒ en KHz. - Dans l'exemple suivant, j'ai utilisé une self de lissage démontée d'une alimentation à découpage.
Si l'on procède au calcul mentionné ci-dessus, cela nous donne : L = 4570 / 1254 = 3,644338118E0 soit 3.644µH - Enfin, pour vérifier tout ceci avec une self (Figure 3) de valeur connue (marquage "221"), j'ai renouvelé la procédure, et le résultat est le suivant :
le marquage "221" signifie que l'inductance est de 220 µH. En effectuant la mesure puis le calcul comme précédemment, la fréquence affichée sur le générateur m'a indiqué la valeur de 20,87 KHz, ce qui nous donne : L = 4570 / 20,87 = 218,9746047E0 soit 218,97µH
Ce n'est peut-être pas de la super précision (seulement 0,47%* de marge d'erreur tout de même...), mais c'est déjà pas mal, et cela nous donne tout de même une idée assez précise de la valeur de l'inductance à tester.
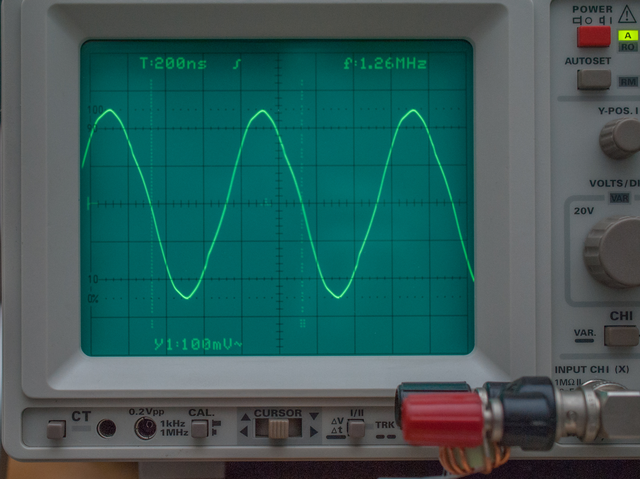

Ci-dessus (Figures 4 et 5) vous pouvez voir la forme du signal d'origine quasiment sinusoïdal lors du test de la self de 220µH, ainsi que les fréquences affichées respectivement par :
- la mesure de l'oscilloscope : 1,26MHZ
- la mesure affichée par le GBF : 1254,5KHz
- la mesure affichée par le fréquencemètre : 1254,457KHZ
J'aime bien vérifier la précision de mes mesures...
La théorie étape par étape :
Dans un premier temps, schématisons le circuit (figure 6)...
La résistance de 50Ω représente la résistance interne (idéale) du générateur, lui-même délimité par les pointillés. L'inductance à mesurer se trouve donc tout naturellement à l'extérieur de cette délimitation. Lorsque le générateur est "à vide" c'est-à-dire sans charge, la résistance interne devient négligeable et l'on retrouve donc la tension maximum en sortie (Vgen = 1Vc/c).
Dans la pratique et pour vous garantir une meilleure précision, il convient de vérifier l'impédance réelle du générateur et de son cordon coaxial de liaison, car selon celui que l'on utilise (longueur et impédance propre du câble...) l'impédance résultante à l'entrée de l'osciloscope peut être très différente des 50 Ω utilisés dans les calculs décrits ci-dessous.
Pour exemple, en utilisant un cordon coaxial d'une longueur de 1,20 m et d'impédance inconnue, j'obtiens une impédance en sortie de câble de 53,14 Ω
Pour calculer cette valeur, j'ai utilisé la procédure suivante : "Exemple 2 : la sortie 50 Ω d'un générateur basse fréquence (GBF)"
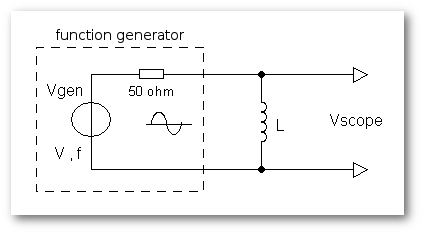
Lors du raccordement de l'inductance (L) à mesurer, nous nous trouvons alors en présence d'un circuit de type RL classique.
Vscope représente la tension à mesurer par l'oscilloscope.
La formule (figure 7) du concepteur de ce procédé est la suivante :

Elle peut paraître compliquée comme cela au premier regard, et j'avoue que j'ai eu la même réaction. Cependant, ce ne sont ici que des "simplifications". Pour comprendre le principe de la mesure avec cette équation, j'ai en fait pris le problème à l'envers :
J'ai effectué les calculs avec des valeurs connues pour l'inductance ainsi que pour la fréquence du générateur, ceci afin de voir où cela allait me mener, et vous aller voir, c'est excessivement simple !
![formule finale [350x152px]](/images/stories/Articles/Mesure/Manipulations/formule%20finale_[350x152px].png)
Procédons par étapes :
D'après ma dernière mesure citée à l'alinéa 11, je connais :
- la valeur de mon inductance : L = 218,97µH
- la fréquence du générateur : ƒ = 20,87 KHz
- la résistance interne du générateur : R = 50Ω
- la pulsation radiale (en rad/s) : ω = 2*π*ƒ
- à titre purement indicatif, j'en déduis la valeur de la réactance* de la self pour la fréquence ƒ indiquée ci-dessus :
XL = ω*L = 2*π*ƒ*L = 28,71355304E0 soit 28,71Ω - et la valeur du courant en appliquant la Loi d'Ohm :
I = Vscope/XL = 0,5/28,71 = 17,41337964E-3 soit 17,41mA
*en régime sinusoïdal, on parle de réactance [Ω] et non de résistance, mais cela ne change rien lorsque l'on applique la Loi d'Ohm...
J'effectue mon calcul avec ces valeurs connues et cela me donne ceci avec la formule simplifiée (figure 8) soit :
[2*π*ƒ*L]/[racine(R²+(2*π*ƒ)²L²] = 497,9959937E-3 ce qui équivaut à 498mV, ou encore quasiment 0,5V et donc la moitié de la tension d'origine du GBF (voir alinéa 3) !
→ Ainsi |Vscop/Vgen| = ½
Mais c'est intéressant cela... cela correspond exactement à la valeur que l'on me demande d'ajuster à l'alinéa 8 dans la seconde phase de la procédure !
Voici donc pourquoi il est nécessaire de procéder à cet ajustement primordial, car la suite des calculs en découle directement !
Et voici cette suite de calculs (que j'e rappelle pour une meilleure compréhension...) permettant de connaître la valeur d'une inductance inconnue (figure 9). Voilà donc pourquoi dans cette seconde série d'équations l'on calcule la valeur de l'inductance avec seulement la moitié de la tension d'origine (500mV au lieu de 1V).
![formule2 développée [606x351px]](/images/stories/Articles/Mesure/Manipulations/formule2_développée_[606x351px].png)
La suite est vraiment simple, je l'ai fait à l'alinéa 11, il suffit juste de calculer la valeur de L selon la formule suivante :
L(H) = 4,57/ƒ(Hz)
Le soucis du petit détail :
◊ En fait, lors de la simplification finale, je ne trouve pas la valeur de [4,57], mais plutôt 4,594407462E0 ce qui fausse quelque peu le résultat de l'équation développée en figure 9. Avec ce coefficient plus précis, j'obtiens alors comme valeur d'inductance 220,1441046E-6 ce qui équivaut à la valeur de 220,14µH au lieu des 218,97µH trouvés précédemment à l'alinéa 11. La tolérance n'est plus de 0,47% mais de -0,064%* .
Voilà pourquoi dans les calculs que j'ai effectués lors de la rédaction de cet article mes chiffres sont représentés selon la notation scientifique. Après, libre à vous de simplifier à votre guise en limitant le nombre de décimales, tout en sachant que cela faussera inéluctablement vos résultats.
Fin de la démonstration !
J'avais en effet annoncé au début de cet article qu'il n'y aurait pas de formules mathématiques, mais je ne pouvais pas vous abreuver d'une formule toute faite, pratique du reste, mais pas vraiment compréhensible de tous sans un minimum d'explications complémentaires.
J'espère vivement que cet article vous a intéressé tout autant que je l'ai été. J'ai pris comme à mon habitude grand plaisir à le réaliser, dans le seul but du transfert de la connaissance ainsi que de mon expérience personnelle.
Philippe.
*Note de correction : Merci à Philippe B. qui m'a rendu compte d'une erreur de décimales qui s'étaient "glissées" dans mon explication des tolérances.
Source:



